『이 공식도 외워두면 편해요!』
지난 시간에 이어 오늘도 필요한 공식을 소개해드리려고 합니다!
포물선과 접선으로 둘러싸인 도형의 면적입니다.
이것을 응용하면 두 개의 포물선사이의 공통접선에 대한 면적을 구할 수 있습니다.
그리고 3차 이상의 함수에 대해서는 어떻게 되는지 한 번 알아보도록 하겠습니다!
본문 읽기 전에 본수학으로 공부한 후기도 읽어주세요!
다시 한 번 중요한 부분은
수학2에서 다루는 함수는 모두 다항함수라는 점입니다!
다항함수는 함수의 중요한 특징을 갖고 있기 때문입니다!
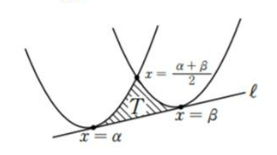
포물선과 두 접선으로 둘러싸인 도형의 면적
좌표평면에 포물선 \(y=ax^{2}+bx+c\; (a\neq0)\)상의 \(x\)좌표가 \(\alpha,\; \beta \; (\alpha <\; \beta)\)가 되는 점을 각각 \(A,\; B\)라 하고 \(A,\; B\)에 대한 포물선의 접선을 각각 \(l_{A},\; l_{B}\)라 하자. \(l_{A},\; l_{B}\)의 교점의 \(x\)좌표는 \(\cfrac{\alpha+\beta}{2}\)이고 포물선과 직선 \(AB\)로 둘러싸인 도형의 면적을 \(S\), 포물선과 \(l_{A},\; l_{B}\)로 둘러싸인 도형의 면적을 \(T\)라 하면 다음을 알 수 있다. $$S=\cfrac{\vert a \vert}{6}(\beta-\alpha)^{3}$$ $$T=\cfrac{\vert a \vert}{12}(\beta-\alpha)^{3}$$ 이 때 \(\alpha, \beta\)에 관계없이 다음이 성립한다. $$S:T=2:1$$
같은 형태의 포물선과 공통접선으로 둘러싸인 도형의 면적
좌표평면에 같은 형태의 포물선이 있다고 하자.
\(y=ax^{2}+bx+c \;(a \neq 0)\)
\(y=ax^{2}+Bx+C\)
두 포물선의 공통접선을 \(l\)이라 하고 두 포물선과 \(l\)의 교점의 \(x\)좌표를 각각 \(\alpha, \; \beta \; (\alpha<\beta)\)라 하자. 이 때 두 포물선의 교점의 \(x\)좌표는 \(\cfrac{\alpha+\beta}{2}\)이고 두 포물선과 \(l\)로 둘러싸인 도형의 면적을 \(T\)라 하면 다음과 같다. $$T=\cfrac{\vert a \vert}{12}(\beta-\alpha)^{3}$$
3차 이상의 함수 그래프와 접선으로 둘러싸인 도형의 면적
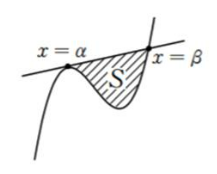
(1) 3차함수의 그래프와 접선으로 둘러싸인 도형의 면적
$$y=ax^{3}+bx^{2}+cx+d \; (a\neq0)$$
$$y=mx+n$$
좌표평면에 3차함수의 그래프와 직선이 \(x\)좌표가 \(\alpha\)의 점에서 접하고 \(x\)좌표가 \(\beta\)의 점에서 교점을 갖는다고 하자. 이 때 3차함수와 직선으로 둘러싸인 도형의 면적을 \(S\)라 하면 다음과 같다. $$S=\cfrac{\vert a \vert }{12}(\beta-\alpha)^{4}$$
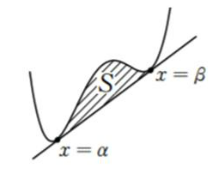
(2) 4차함수의 그래프와 접선으로 둘러싸인 도형의 면적
$$y=ax^{4}+bx^{3}+cx^{2}+dx+e \; (a\neq0)$$
$$y=mx+n$$
좌표평면에 4차함수의 그래프와 직선이 \(x\)좌표가 \(\alpha\)의 점에서 접하고 \(x\)좌표가 \(\beta\)의 점에서 교점을 갖는다고 하자. 이 때 4차함수와 직선으로 둘러싸인 도형의 면적을 \(S\)라 하면 다음과 같다. $$S=\cfrac{\vert a \vert }{30}(\beta-\alpha)^{5}$$
연습문제
(1) 포물선과 두 접선으로 둘러싸인 도형의 면적을 증명하여라. 그리고 그것을 이용하여 같은 형태의 포물선과 공통접선으로 둘러싸인 도형의 면적를 증명하여라.
(2) 3차 이상의 함수 그래프와 접선으로 둘러싸인 도형의 면적을 증명하여라.
최상위권 학생들을 위한 본고사 문제 제작소
본수학 네이버 카페 cafe.naver.com/bornmath
본수학 네이버 블로그 blog.naver.com/flytome91
본수학 유튜브 https://www.youtube.com/@born_math
본수학 문제집 주문하러 가기 https://naver.me/5Luk3pbL
본수학 동영상 강의 보러 가기 https://bornmath.liveklass.com/
'고등수학 개념 > 수학Ⅱ' 카테고리의 다른 글
| [수학Ⅱ]18.정적분과 면적 (0) | 2024.05.14 |
|---|---|
| [수학Ⅱ]17.적분공식 (0) | 2024.05.13 |
| [수학Ⅱ]16.정적분의 기본성질 (0) | 2024.05.10 |
| [수학Ⅱ]15.정적분의 정의 (0) | 2024.05.09 |
| [수학Ⅱ]14.다항함수의 적분과 적분 성질 (0) | 2024.05.08 |