[수학Ⅱ]18.정적분과 면적

 

 

『정적분은 면적이다!』

 

정적분이 가지는 기하학적인 의미는 무엇일까요?

바로 곡선과 $x$축사이의 면적을 뜻합니다.

 

 

자세한 사항은 미적분 단원에서 공부할 예정입니다만

적분은 미세한 막대기를 곡선에 알맞게 쌓은 값으로

곡선과 $x$축사이의 면적을 지칭합니다.

 

그럼 정적분의 기하학적인 의미와 그 응용에 대해 알아보도록 하겠습니다!

---

본문 읽기 전에 본수학으로 공부한 후기도 읽어주세요!

 

과학고 수학 내신 1등 후기 보러가기

 

서울대 합격 후기 보러가기

 

---

---

• $x$축과 곡선사이의 면적
• 두 개의 곡선사이의 면적
• 두 개의 곡선사이의 면적2
• 연습문제

---

$x$축과 곡선사이의 면적

좌표평면에 대해 구간 $a\le x\le b$에서 $f(x)\ge 0$이라 하자. 곡선 $y=f(x)$와 $y=0$ 및 두 직선 $x=a,x=b$로 둘러싸인 도형의 면적을 $S$라 하면 다음과 같다 $$S={\int }_a^{b}ydx={\int }_a^{b}f(x)dx$$ 좌표평면에 대해 구간 $a\le x\le b$에서 $f(x)\le 0$이라 하자. 곡선 $y=f(x)$와 $y=0$ 및 두 직선 $x=a,x=b$로 둘러싸인 도형의 면적을 $S$라 하면 다음과 같다 $$S={\int }_a^b(-y)dx=-{\int }_a^{b}f(x)dx$$

정적분의 기하학적 의미

정적분의 기하학적인 측면은 $x$축과 곡선사이의 면적이라고 언급했습니다.

다만 주의해야 할 점은 $x$축 아래에 있는 곡선에 대해서는 면적에 $-1$을 곱한 값입니다.

 

두 개의 곡선사이의 면적

좌표평면에 대해 구간 $a\le x\le b$에서 $f(x)\ge g(x)$이라 하자. 곡선 $y=f(x)$와 $y=g(x)$및 두 직선 $x=a,x=b$로 둘러싸인 도형의 면적을 $S$라 하면 다음과 같다. $$S={\int }_a^b\{f(x)-g(x)\}dx$$

 

두 개의 곡선 사이의 면적

 

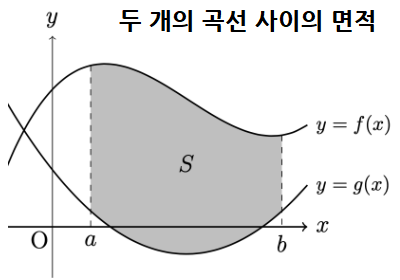
두 개의 곡선사이의 면적은 정적분의 기하학적인 측면으로 당연한 결과입니다!

 

두 개의 곡선사이의 면적2

$a<b$라 하자. 좌표평면에 대해 곡선 $y=f(x)$와 $y=g(x)$ 및 두 직선 $x=a,x=b$로 둘러싸인 도형의 면적을 $S$라 하면 다음을 알 수 있다. $$S={\int }_a^b|f(x)-g(x)|dx$$ 특히 $a\le b$에 대해 $f(x)$와 $g(x)$의 대소관계가 바뀌지 않을 때 다음을 알 수 있다. $$S={\int }_a^b|f(x)-g(x)|dx=|{\int }_a^b\{f(x)-g(x)\}dx|$$

 

 

 

위의 공식들은 두 개의 곡선의 대소관계를 모르거나 교점이 있는지 없는지 관계없이 일반적인 곡선사이의 면적을 나타냅니다.

 

연습문제

(1) 두 개의 곡선사이의 면적을 증명하여라.

(2) 두 개의 곡선사이의 면적2에서 대소관계가 바뀔 경우 성립하지 않는 예시를 보여라..

 

 

최상위권 학생들을 위한 본고사 문제 제작소

본수학 네이버 카페 cafe.naver.com/bornmath

본수학 네이버 블로그 blog.naver.com/flytome91

본수학 유튜브 https://www.youtube.com/@born_math

본수학 문제집 주문하러 가기 https://naver.me/5Luk3pbL

본수학 동영상 강의 보러 가기 https://bornmath.liveklass.com/