안녕하세요. 본수학 저자입니다.
오늘은 조합의 정의와 성질에 대해 알아보도록 하겠습니다.
경우의 수 단원에서 가장 어려운 부분이 조합입니다. 조합이란 무엇인지 정의를 확실히 공부해 놓으면 고난이도 문제에 대응할 수 있으리라 생각됩니다.
목차
1. 조합
1.1 조합이란?
조합은 순서를 생각하지 않고 그룹을 만든다는 뜻입니다.
순서를 생각하지 않고 뽑는 방법을 조합이라 한다. 서로 다른 \(n\)개에서 서로 다른 \(r\)개를 뽑아 만드는 조합을 \(n\)개에서 \(r\)개를 뽑는 조합이라 하고 그 총 수를 \(_{n}C_{r}\)이라 나타낸다.
앞서 순열이랑 다른 부분은 순서를 생각하지 않는다는 것입니다. 예를 들어 1부터 5까지의 숫자가 적힌 공이 5개 있는데 여기서 3개를 뽑는 경우의 수를 구하는 것과 같습니다. 순열을 구하는 것이라면 즉, 첫 번째, 두 번째, 세 번째 이렇게 오는 경우의 수를 구하는 것이므로 \((1, 2, 3)\), \((1, 3, 2)\), \((2, 3, 1)\), \((2, 1, 3)\), \((3, 1, 2)\), \((3, 2, 1)\)모두 다른 경우지만 조합에서는 순서가 아닌 그룹을 나타내므로 모두 같은 한 가지의 경우로 취급합니다.
여기서 기호 \(C\)가 나오는데 이것은 조합의 영어인 Combination에서 따왔습니다.
1.2 \(_{n}C_{r}\)의 계산
조합은 순서대로 나열하는 것이 아닌 그룹을 만드는 것이라고 설명했는데 정확히 조합의 기호는 어떻게 계산하면 되는지 알아보도록 하겠습니다.
\(n\)을 자연수, \(r\)을 \(0\leq r \leq n\)인 정수라 할 때 \(_{n}C_{r}\)을 다음과 같이 정의한다.
\( \begin{align}
\displaystyle _{n}C_{r} & = \cfrac{n(n-1)(n-2)\cdots (n-r+1)}{r!} \\
& = \frac{n!}{r!(n-r)!} \\
& = \frac{_{n}P_{r}}{r!}
\end{align} \)
특히 \(r=n\)일 때 \(_{n}P_{r}=n!\), \(r=0\)일 때 \(_{n}P_{0}=1\)
1.2 \(_{n}C_{r}\)의 성질
조합의 성질은 경우의 수를 세는 단순 계산을 넘어 다양한 분야에 이용되고 있습니다.
【증명】
(1) \(n\)개 중에서 \(r\)개를 포함하는 그룹을 만드는 것은 자연스럽게 나머지 \(n-r\)개를 포함하는 그룹을 만드는 것과 같으므로 조합의 정의에 의해 성립하는 것을 알 수 있다.
(2) \(n\)개 중에서 \(r\)개를 포함하는 그룹을 만드는 것은 특정 한 개를 고르고, 그것이 포함되어 있는 그룹을 세는 것과 포함되어 있지 않은 그룹의 개수를 세는 것의 합과 같다. 따라서 특정 한개를 고르고 그것이 포함되어 있는 그룹은 \(n-1\)개 중에서 \(r-1\)개를 포함하는 그룹을 만드는 것과 같고 포함되어 있지 않는 그룹은 \(n-1\)개 중에서 \(r\)개를 만드는 것과 같으므로 조합의 정의에 의해 성립하는 것을 알 수 있다.
위의 성질을 \(_{n}C_{r}\)의 정의를 이용하여 증명하여라.
1.3 조합의 관계식
(1) \(n\), \(k\)를 자연수,\(1 \leq k \leq n\)일 때 다음이 성립한다.
\(k_{n}C_{r}=n_{n-1}C_{k-1}\)
【증명】
\( \begin{align}
\displaystyle k_{n}C_{k} & = k\frac{n!}{k!(n-k)!} \\
& = n\frac{(n-1)!}{(k-1)!(n-k)!} \\
& = n_{n-1}C_{k-1}
\end{align} \)
2. 같은 것을 포함하는 순열
2.1 같은 것을 포함하는 순열의 총 수
순열은 순열인데 같은 것을 포함하는 순열은 어떻게 셀까요? 특이하게도 조합을 이용하여 순열을 계산합니다.
\(A\)가 \(p\)개, \(B\)가 \(q\)개 총 \((p+q)\)개의 순열의 총 수는 다음과 같다.
\(_{p+q}C_{p}=_{p+q}C_{q}=\cfrac{(p+q)!}{p!q!}\)
【증명】
우선 같은 \(p\)개와 \(q\)개가 서로 다르다고 생각하자. 그럼 \(p+q\)개의 순열은 \((p+q)!\)이다. 그 후 서로 다른 \(p\)개를 같이 보면 \(p!\)만큼 같은 개수가 생긴다. 예를 들어 \(p_{1}\)과 , \(p_{2}\)가 서로 다르고 하자. 그러면 \((a, \;p_{1}, \;b,\; p_{2})\)와 \((a,\; p_{2},\; b,\; p_{1})\)는 서로 다른 열이 된다. 하지만 \(p_{1}\)과 \(p_{2}\)가 같다고 생각하면 2개 즉 \(2!\)만큼 같기 때문에 \(\cfrac{2}{2!}=1\)개가 된다. 이처럼 \(q\)개도 서로 같다고 생각하면 구하고자 하는 순열은 다음과 같다. \(\cfrac{(p+q)!}{p!q!}=_{p+q}C_{p}=_{p+q}C_{q}\)
\(A\)가 \(p\)개, \(B\)가 \(q\), \(C\)가 \(r\)개 총 \((p+q+r)\)개의 순열의 총 수는 다음과 같다.
\(\cfrac{(p+q+r)!}{p!q!r!}\)
【증명】
위와 마찬가지로 동일하게 증명가능하다.
같은 것을 포함하는 순열의 총 개수는 다음의 순서대로 구할 수 있다.
(1) 전부 서로 다르다고 보고 순열의 총 개수 \(N\)을 구한다.
(2) \(N\)을 같은 것의 개수의 팩토리얼로 나눈다.
위의 일반화된 식을 증명하여라.
2.2 평면에서의 최단경로의 개수
유한집합의 원소의 개수를 셀수 있으면 유한집합의 연산 특히 합집합의 원소의 개수도 셀 수 있습니다. 우선 집합 두 개의 합집합의 원소의 개수는 어떻게 되는지 알아보도록 하겠습니다.
\(m \times n\)개의 바둑판으로 이루어진 길이 있을 때 \(A\)에서 \(B\)로 가는 최단경로의 개수는 다음과 같다.
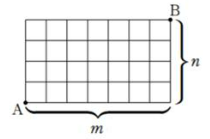
\(\cfrac{(m+n)!}{m!n!}=_{m+n}C_{m}=_{m+n}C_{n}\)
【증명】
평면에서의 최단경로의 개수는 \(\rightarrow\)가 \(m\)개, \(\uparrow\)가 \(n\)개인 같은 것을 포함하는 순열과 같다. 따라서 구하고자 하는 경우의 수는 다음과 같다.
\(\cfrac{(m+n)!}{m!n!}=_{m+n}C_{m}=_{m+n}C_{n}\)
전체 집합 \(U = \{1, 2, 3, 4, 5\}\)이고 \(U\)의 부분집합 \(A=\{1, 2, 3\}\)이 있을 때 \(A\)의 여집합 \(A^{c}\)를 구하여라.
【해설】
- \(U\)는 \(\{1, 2, 3\}\)와 \(\{4, 5\}\)의 합집합으로 구성되므로 \(A^{c}\)는 \(\{4, 5\}\)이다.
3. 중복조합
3.1 중복조합이란?
조합에서 가장 어려운 파트인 중복조합에 대해 알아보도록 하겠습니다.
서로 다른 \(n\)개 중 중복을 허용하여 \(r\)개를 고르는 경우의 수를 중복조합이라 하며 \(_{n}H_{r}\)이라 나타낸다..
예를 들어 사과하고 배 두 종류의 과일이 있는데 이 중에 중복을 허용하여 3개를 택하는 경우는(배, 배, 배), (배, 배, 사과),(배, 사과, 사과), (사과, 사과, 사과) 총 4개입니다.
3.2 중복조합의 개수
그러면 중복조합 \(_{n}H_{r}\)은 어떻게 계산되는지 알아보도록 하겠습니다!중복조합 \(_{n}H_{r}\)는 다음과 같다.
\(_{n}H_{r}=_{n+r-1}C_{r}=\cfrac{(n+r-1)!}{(n-1)!r!}\)
【증명】
\(r\)개를 \(a_{1}, a_{2}, \cdots, a_{r}\)라 하고 칸막이를 이용하여 서로 다른 \(n\)개로 대응시킬 수 있다. 위의 예시를 예로 들면 3개를 뽑으므로 \(a_{1}, a_{2}, a_{3}\)라 하고 칸막이 / 를 이용하여 두 곳으로 구분지을 수 있다. \((/ a_{1}, a_{2}, a_{3})\) \((a_{1},/ a_{2}, a_{3})\) \((a_{1}, a_{2},/ a_{3})\) \((a_{1}, a_{2}, a_{3}/)\) 칸막이 / 를 기준으로 앞에는 사과, 뒤는 배로 나눌 수 있다. 칸막이 / 앞이나 뒤에 아무것도 없으며 개수는 0개이다. 위와 같은 경우의 수는 \(a_{1}, a_{2}, a_{3}\)를 같다고 보고 칸막이를 포함한 순열의 개수이므로 \(_{4}C_{3}\) 또는 \(_{4}C_{1}\)이다. 이를 일반화하면 \(r\)개에 구분선 \(n-1\)개를 추가하여 \(r\)개를 같게 보는 순열의 개수이므로 다음을 알 수 있다.
\(_{n}H_{r}=_{n+r-1}C_{r}=\cfrac{(n+r-1)!}{(n-1)!r!}\)
빨강, 파랑, 검은 색 3종류의 공이 여러개가 있다. 이 중에서 중복을 허용하여 4개의 공을 꺼내는 경우의 수를 구하여라.
【해설】
- 구하고자 하는 경우의 수는 \(_{3}H_{4}=_{6}C_{4}=15\)가지다.
오늘의 학습 정리
【조합】
순서를 생각하지 않고 뽑는 방법을 조합이라 한다. 서로 다른 \(n\)개에서 서로 다른 \(r\)개를 뽑아 만드는 조합을 \(n\)개에서 \(r\)개를 뽑는 조합이라 하고 그 총 수를 \(_{n}C_{r}\)이라 나타낸다.
\(_{n}C_{r}=_{n}C_{n-r}== \frac{n!}{r!(n-r)!}\)
【같은 것을 포함하는 순열】
\(A\)가 \(p\)개, \(B\)가 \(q\)개 총 \((p+q)\)개의 순열의 총 수는 다음과 같다.
\(_{p+q}C_{p}=_{p+q}C_{q}=\cfrac{(p+q)!}{p!q!}\)
【중복조합】
서로 다른 \(n\)개 중 중복을 허용하여 \(r\)개를 고르는 경우의 수를 중복조합이라 하며 \(_{n}H_{r}\)라 나타낸다.
\(_{n}H_{r}=_{n+r-1}C_{r}=\cfrac{(n+r-1)!}{(n-1)!r!}\)
조합은 가장 어려운 단원이고 킬러문항으로도 많이 나오기 때문에 많은 연습이 필요로 합니다.

(1) \(n\)을 자연수, \(r\)을 \(0 \leq r \leq n\)이 되는 정수라 할 때
\(_{n}C_{r}=_{n}C_{n-r}\)
(2) \(n\)을 2이상의 자연수, \(r\)을 \(1 \leq r \leq n-1\)이 되는 정수라 할 때
\(_{n}C_{r}=_{n-1}C_{n-r}+_{n-1}C_{r}\)