안녕하세요. 본수학 저자입니다.
오늘은 순열의 종류에 대해 알아보도록 하겠습니다.
경우의 수하면 순열과 조합, 이 두 가지의 케이스로 경우의 수를 구하는데 오늘은 그 중 하나인 순열에 대해 알아보고 순열에는 어떠한 종류가 있는지 알아보도록 하겠습니다.
목차
1. 순열
1.1 순열이란?
순열은 순서대로 열을 세운다는 뜻입니다.
순서를 생각하여 1열로 나열하는 것을 순열이라 한다. 서로 다른 \(n\)개의 물건에서 서로 다른 \(r\)개를 뽑아 나열하는 순열을 \(n\)개에서 \(r\)개를 뽑는 순열이라 하고 총 수를 \(_{n}P_{r}\)이라 한다.
우리는 이미 이전 학습에서 팩토리얼을 배울 때 다룬 적이 있습니다!
1부터 10까지 적힌 10개의 공을 일렬로 나열하는 방법은 \(10!\)이라고 한 거요!
근데 1부터 10까지 적힌 10개의 공 중 3개를 일렬로 나열하는 방법은 몇가지일까요?
처음에 올 수 있는 경우 10가지, 그 다음 두 번째에 올 수 있는 경우 9가지, 그 다음 세 번째에 올 수 있는 경우 8가지로 곱의 법칙을 사용해서 \(10 \times 9\times 8 =720\)가지입니다!
이것을 기호로 \(_{10}P_{3}\)으로 나타냅니다.
1.2 \(_{n}P_{r}\)의 계산
순열은 순서대로 나열하는 것이라고 배웠는데 정확히 순열의 기호는 어떻게 계산하면 되는지 알아보도록 하겠습니다.
\(n\)을 자연수, \(r\)을 \(0\leq r \leq n\)인 정수라 할 때 \(_{n}P_{r}\)을 다음과 같이 정의한다.
\( \begin{align}
\displaystyle _{n}P_{r} & = n(n-1)(n-2) \cdots (n-r+1) \\
& = \frac{n!}{(n-r)!}
\end{align} \)
특히 \(r=n\)일 때 \(_{n}P_{r}=n!\), \(r=0\)일 때 \(_{n}P_{0}=1\)
2. 원순열
2.1 원순열이란?
초등학생 때 실에 여러가지 비즈를 끼워 목거리를 만든 적이 있을 거예요!
(가정 수업 때 다들 있지 않았나요...?)
일렬로 비즈를 세우는 경우의 수와 줄에 끼워 목걸이를 만드는 경우의 수는 다릅니다!
왜냐면 목걸이는 돌아가기 때문이죠!
예를 들어 1-2-3 이렇게 세우는 것과 2-3-1 이렇게 세우는 것은 다르지만 줄에 끼워 목걸이로 만들면 모두 같은 경우의 수가 됩니다!
원형으로 나열하는 것을 원순열이라 한다. 회전하여 같은 것은 같은 방법이라 간주한다.
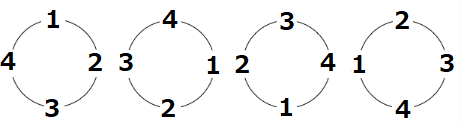
2.2 원순열의 총 수
그러면 원순열의 경우의 수는 어떻게 구하는지 알아보도록 하겠습니다.【증명】
원순열을 일반 순열과 동일시하기 위해 한 개를 골라 고정을 시키자. 이것을 기준으로 시계방향으로 나열하면 일반적인 순열이 되므로 구하고자 하는 경우의 수는 \((n-1)!\)이다.
3명의 남자 A, B, C와 3명의 여자 D, E, F가 원테이블에 앉는다고 하자.
- 구하고자 하는 경우의 수는 \((6-1)!=5\times 4\times 3\times 2\times 1 =120\)가지다.
3명의 남자 A, B, C와 3명의 여자 D, E, F가 원테이블에 앉는다고 하자. A와 D가 마주보고 앉는 경우의 수는 몇 가지인가?
3. 중복순열
3.2 중복순열의 총 수
서로 다른 \(n\)개에서 \(r\)개를 뽑는 중복순열의 총 수는 \(n^{r}\)이다.
【증명】
첫 번째 올 수 있는 경우의 수 \(n\)개, 두 번째 올 수 있는 경우의 수도 \(n\)개, 마찬가지로 \(r\)번째까지 올 수 있는 경우의 수도 \(r\)개이므로 곱의 법칙에 의해서 \(n^{r}\)개다.
오늘의 학습 정리
【순열】
\( _{n}P_{r}= \cfrac{n!}{(n-r)!}\)
【원순열】
\((n-1)! \)
【중복순열】
\( n^{r} \)
경우의 수의 가장 기본적인 원소의 개수와 그에 따른 여러가지 정리에 대해 알아봤습니다. 다음 시간부터는 본격적인 경우의 수 단원이 시작되므로 오늘의 내용을 꼭 숙지해주시길 바라겠습니다.

서로 다른 \(n\)개의 원순열의 총 수는 \((n-1)!\)이다.