
『내가 이만큼 변하면 너는 얼만큼 변할거야?』
드디어 미분과 적분이라는 파트에 들어왔습니다.
앞서 공부한 함수의 극한과 연속성에서 다룬 개념을 가지고
미분과 적분에 대해 공부할 예정입니다.
미분에 들어가기 앞서 우리는 변화율에 대해 이야기 해보겠습니다.
변화율에는 크게 평균변화율과 순간변화율 두 가지가 있습니다.
학교 시험의 평균이라고 하면 모든 점수를 더해 학생수로 나눈 값입니다.
즉 평균이라는 개념은 평평하고 균일한 뜻이 함축되어 있습니다.
따라서 평균변화율이라 하면 일정하게 변화하였을 때 얼만큼 변하는지 나타내는 것입니다.
순간변화율은 말 그대로 어느 순간 변화하였을 때 얼만큼 변하는지를 나타내는 것입니다.
그럼 구체적으로 무슨 뜻인지 살펴보도록 하겠습니다.
그 전에 중요한 건 수학2에서 다루는 함수는 모두 다항함수입니다.
\(y=x^3+3x^2+2\) 이런 함수죠!
그 이유는 다항함수는 모두 연속이며 미분가능한 함수이기 때문입니다!
자세한 사항은 수학2가 아닌 미분과 적분 시간에 배웁니다!
다시 한 번 중요한 부분은
수학2에서 다루는 함수는 모두 다항함수라는 점입니다!
다항함수는 함수의 중요한 특징을 갖고 있기 때문입니다!
평균변화율
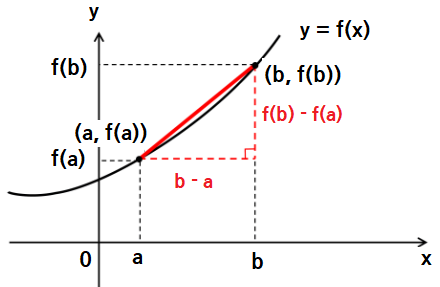
함수 \(y=f(x)\)에 대해 \(x\)의 값이 \(a\)에서 \(b\)까지 증가할 때 \(x\)의 변화율 \(b-a\), \(y\)의 변화율 \(f(b)-f(a)\)의 비 \(\cfrac{f(b)-f(a)}{b-a}\)를 \(x\)가 \(a\)에서 \(b\)까지 변화할 때 함수 \(y=f(x)\)의 평균변화율이라 한다. 이것은 두 점 \((a, f(a))\), \((b, f(b))\)를 지나는 직선의 기울기다.
평균변화율은 두 점사이를 지나는 직선의 기울기를 뜻합니다.
그림으로 나타내면 다음과 같이 나타낼 수 있죠!
극한값
함수 \(f(x)\)에 대해 \(x\)가 \(a\)와 다른 값을 가지면서 무한히 \(a\)에 가까워질 때 \(f(x)\)가 일정한 값 \(\alpha\)에 무한히 가까워지면 \(x \rightarrow a\)일 때 \(f(x)\rightarrow \alpha\) 또는 \(\displaystyle{\lim_{x\rightarrow a}f(x)=\alpha}\)이라 쓰고 \(\alpha\)를 \(x\)가 \(a\)에 무한히 가까워질 때의 함수 \(f(x)\)의 극한값이라 한다.
순간변화율을 배우기 이전에 극한의 개념을 도입하여 극한값을 배워보겠습니다.
극한값은 \(x\)가 특정값에 가까워질 때 \(y\)값 즉 함수값이 어느 특정값에 가까워지면 그 때 그 값을 극한값이라 합니다.
수학2에서는 다항함수 위주로 다루기 때문에 모두 연속인 함수라 가정합니다.
순간변화율
\(x\)의 값이 \(a\)에서 \(a+h\)까지 변화할 때 함수 \(y=f(x)\)의 평균변화율 \(\cfrac{f(a+h)-f(a)}{h}\)에 대해 \(h\)가 무한히 0에 가까워질 때 이 평균변화율이 어느 값에 무한히 가까워지면 그 각한값을 함수 \(y=f(x)\)의 \(x=a\)에 대한 순간변화율 또는 미분계수라 하고 \(f'(a)\)라 나타낸다. $$f'(a)=\displaystyle{\lim_{h\rightarrow 0}\cfrac{f(a+h)-f(a)}{h}}$$
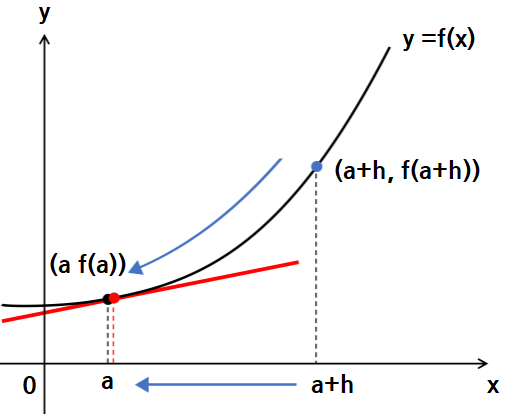
평균변화율에서 \(a\)와 \(b\)사이의 거리가 0에 가까워지면 어떻게 될까요?
평균변화율은 점점 \(x = a\)쪽에서 두 개의 점을 잇는 직선의 기울기가 되겠죠?
점점 두 점 사이의 거리가 0에 가까워지면 \(x = a\)에서의 접선의 기울기가 됩니다!
연습문제
(1) \(y=x^3+3x^2+3\)의 \(x=3\)에서의 미분계수를 구하여라.
(2) \(x\)의 값이 \(a\)에서 \(a+h\)까지 변화하지 않고 \(a\)에서 \(a-h\)까지 변화하는 평균변화율에 대한 미분계수의 정의는 변함이 없는지 생각해보자.
최상위권 학생들을 위한 본고사 문제 제작소
본수학 네이버 카페 cafe.naver.com/bornmath
본수학 네이버 블로그 blog.naver.com/flytome91
본수학 유튜브 https://www.youtube.com/@born_math
본수학 문제집 주문하러 가기 https://naver.me/5Luk3pbL
본수학 동영상 강의 보러 가기 https://bornmath.liveklass.com/
'고등수학 개념 > 수학Ⅱ' 카테고리의 다른 글
| [수학Ⅱ]10.미분의 정의 (0) | 2024.04.29 |
|---|---|
| [수학Ⅱ]9.도함수의 정의 (0) | 2024.04.27 |
| [수학Ⅱ]7.중간값 정리 (0) | 2024.04.22 |
| [수학Ⅱ]6.최댓값과 최솟값의 정리 (0) | 2024.04.19 |
| [수학Ⅱ]5.함수의 연속과 성질 (0) | 2024.04.16 |